Funciones cuadráticas: las parábolas
La gráfica de las funciones polinómicas de segundo grado o funciones cuadráticas son las parábolas.
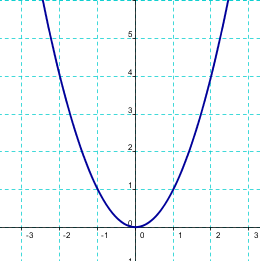
La forma general de la expresión algebraica de la parábola es $y=f(x)=ax^2+bx+c$ donde $a\neq 0$ y tiene las siguientes características:
-
Tiene un eje de simetría en la recta $x=-\frac{b}{2a}$, que pasa por el vértice.
-
La coordenada $x$ del vértice es $x=-\frac{b}{2a}$. Por tanto, el vértice es el punto:
$V=\left (-\frac{b}{2a},f \left( -\frac{b}{2a} \right) \right)$
-
La parábola tiene las ramas hacia arriba si $a>0$ y tiene las ramas hacia abajo si $a<0$.
-
Los coeficientes $b$ y $c$ sólo trasladan la parábola, no cambian su forma.
-
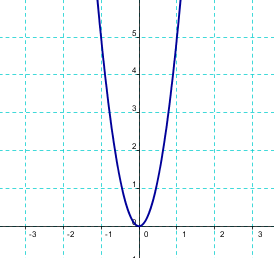
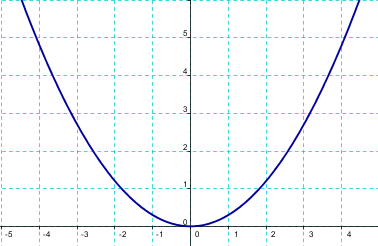
La parábola es más estilizada cuanto mayor es $a$ en valor absoluto:
 |
 |
En la siguiente animación mueve los parámetros $a$, $b$ y $c$ y observa cómo varía la ecuación de la gráfica y deduce cómo influyen $a$ y $c$ en la gráfica.
Después traslada la gráfica y observa qué ocurre con la ecuación.