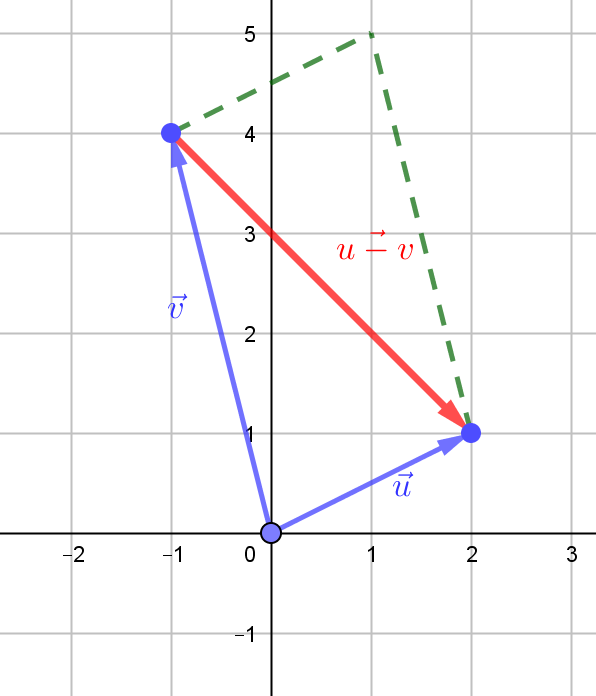
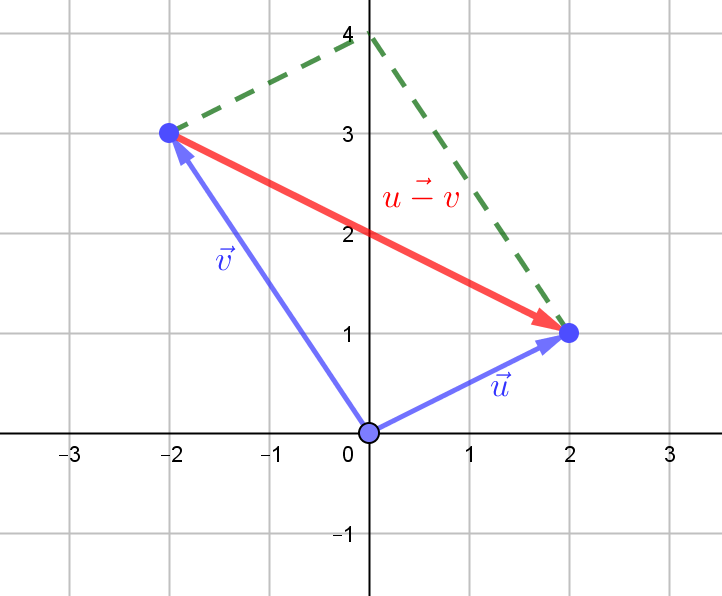
Resta de vectores
Recuerda que restar es lo mismo que sumar el opuesto, es decir, $\vec{u}-\vec{v}=\vec{u}+\left(-\vec{v}\right)$
La resta de dos vectores, $\vec{u}-\vec{v}$ se puede hacer de dos formas distintas:
-
De forma analítica: se restan componente a componente.
-
De forma geométrica: se dibujan los dos vectores con el mismo origen. Se completa el paralelogramo con los dos vectores. La diagonal cuyo origen es el extremo de $\vec{v}$ y extremo es el extremo de $\vec{u}$