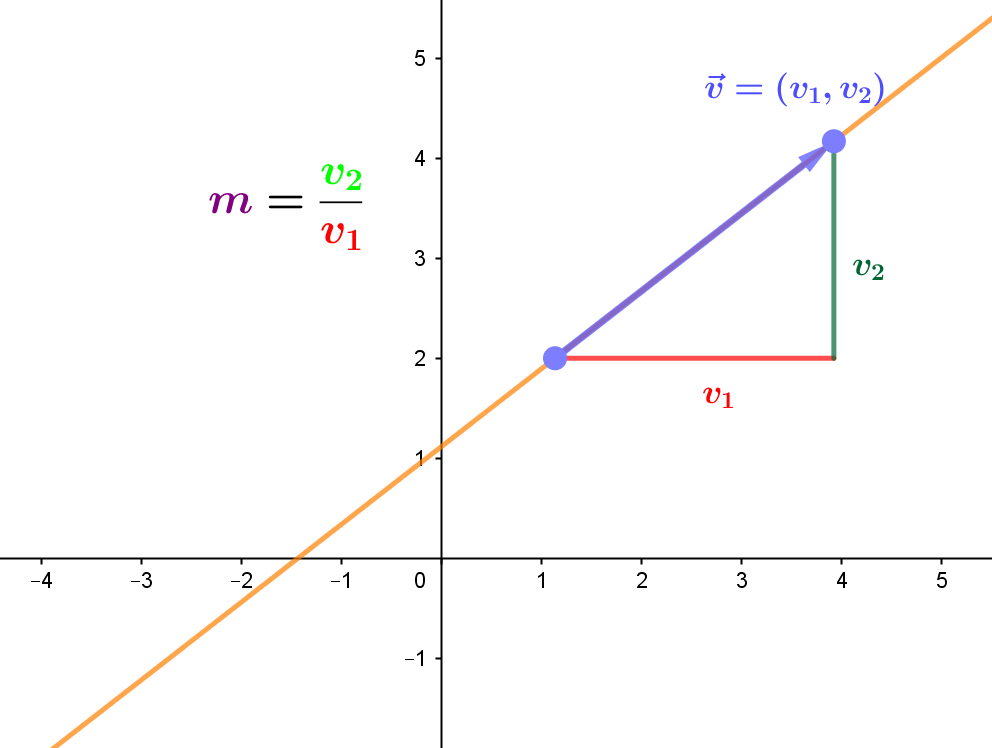
Pendiente de una recta
La pendiente de una recta, que denotaremos con la letra $m$, es la inclinación de la recta. Dados dos puntos $A\left(a_{1},a_{2}\right)$ y $B\left(b_{1},b_{2}\right)$, se define como la variación de de la coordenada $y$, \(\Delta y \) entre la variación de la coordenada $x$, \(\Delta x \).
\[m=\dfrac{b_{2}-a_{2}}{b_{1}-a_{1}}\]
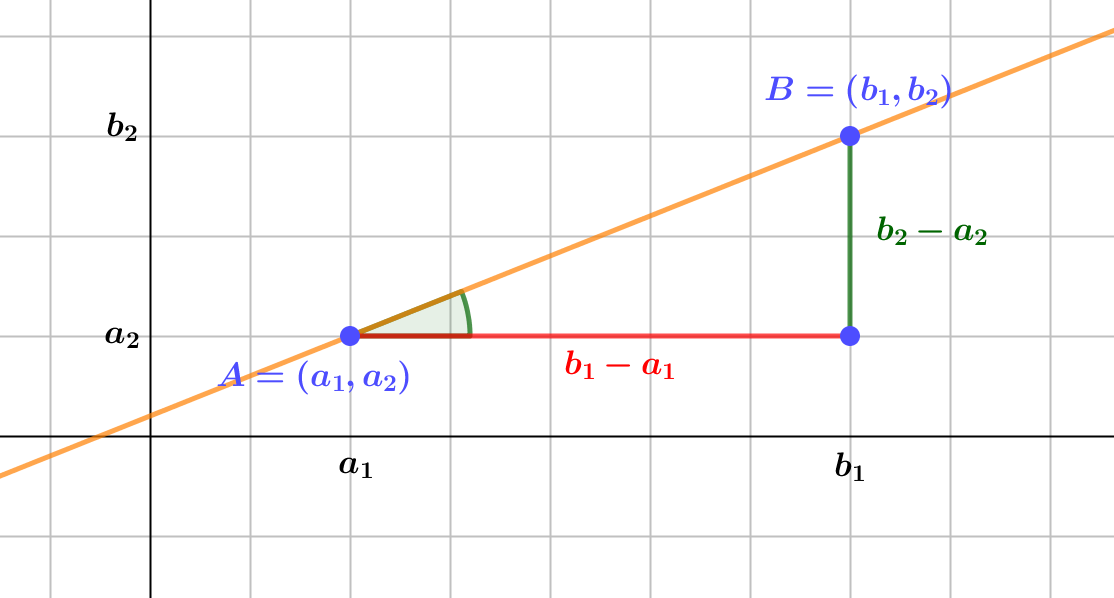
Dado que la pendiente de una recta tiene relación con la inclinación de la recta, ¿qué relación habrá entre el ángulo que forma la recta con el eje de coordenadas (inclinación) y la pendiente de una recta?
Utilizaremos los conceptos básicos de Trigonometría que ya hemos visto. Observa la imagen anterior, según hemos definido la pendiente anteriormente, tenemos que la pendiente es el cateto opuesto dividido entre el cateto continuo del triángulo rectángulo de la imagen. ¿Qué razón trigonométrica relaciona los dos catetos con el ángulo... Efectivamente, la pendiente es la tangente de dicho ángulo, \(\alpha \)
\[ m=\tan (\alpha)\]