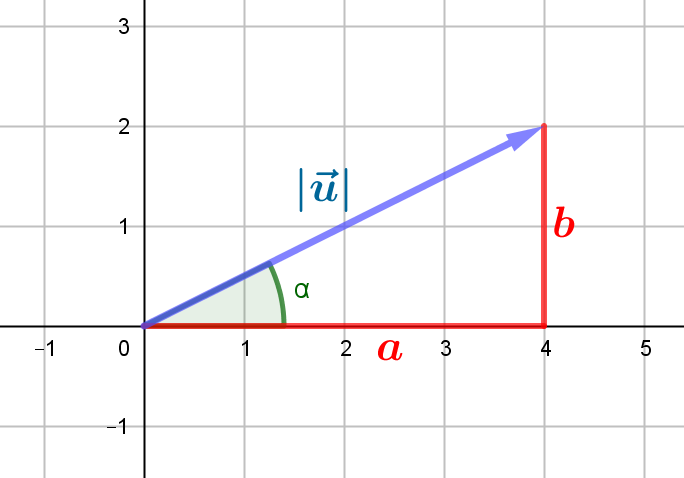
El módulo de un vector $\vec{u}$ es la longitud del vector. Lo denotaremos $\left|\vec{u}\right|$. Para calcular el módulo de un vector dadas sus componentes utilizaremos el teorema de Pitágoras.
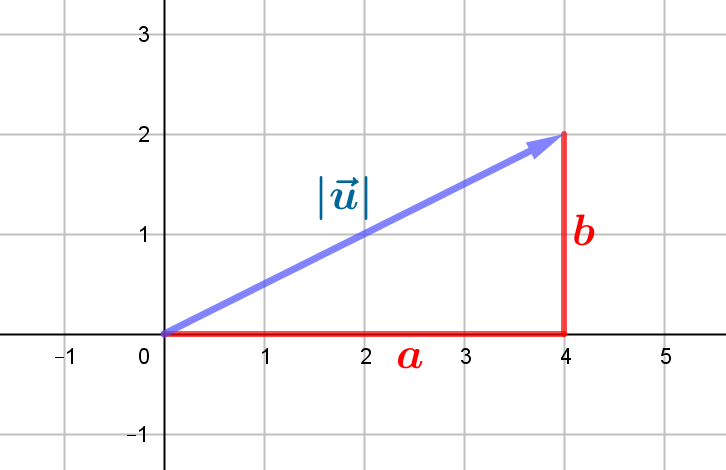
\[\left|\vec{u}\right|=\sqrt{a^{2}+b^{2}}\]
Cuando un vector tiene módulo 1, diremos que es un vector unitario.
Llamaremos argumento, $\alpha$, de un vector, $\vec{u}$, al ángulo que forma el vector con el semieje positivo. Para calcular el argumento de un vector dadas sus coordenadas utilizaremos la tangente.
\[\tan\alpha=\dfrac{b}{a}\Leftrightarrow\alpha=\arctan\dfrac{b}{a}\]
Ojo, que la arcotangente de un número tiene dos soluciones en los primeros $360^{\circ}$ y la calculadora sólo nos da una de ellas, la otra se obtiene sumando $180^{\text{º}}$. Tenemos que tener cuidado y elegir el ángulo correcto que forma nuestro vector dependiendo del cuadrante en el que se sitúe.
¿Cuáles son los argumentos de los vectores $\vec{u}=\left(1,3\right)$ y $\vec{v}=\left(-1,-3\right)$
\[\alpha=\arctan\dfrac{3}{1}=\begin{cases}71,57^{\circ}\\71,57^{\circ}+180^{\circ}=251,57^{\circ}\end{cases}\]
El argumento del vector $\vec{u}=\left(1,3\right)$ es $\alpha=71,57^{\circ}$ porque $\vec{u}$ pertenece al primer cuadrante.
El argumento del vector $\vec{v}=\left(-1,-3\right)$ es $\alpha=251,57^{\circ}$ porque $\vec{v}$ pertenece al tercer cuadrante.
Dados los puntos $A\left(1,4\right)$ y $B\left(2,-5\right)$, calcula:
El vector $\vec{AB}$
El vector $\vec{BA}$
El módulo del vector $\vec{AB}$. ¿Coincide con el módulo del vector $\vec{BA}$?
El argumento de los vectores $\vec{AB}$ y $\vec{BA}$
¿Cómo son los vectores $\vec{AB}$ y $\vec{BA}$?
En los apartados anteriores vimos cómo podíamos calcular el módulo y el argumento de un vector conociendo sus componentes. Ahora vamos con el proceso contrario, cómo hallar las componentes de un vector conociendo su módulo y argumento.
Para calcular las componentes de un vector de módulo $\left|\vec{u}\right|$ y argumento, el ángulo $\alpha$ utilizaremos trigonometría básica. Así:
$a=\left|\vec{u}\right|\cos\alpha$
$b=\left|\vec{u}\right|\sin\alpha$
Calcula las componentes de los vectores cuyos módulos y argumentos son los siguientes:
$\left|\vec{u}\right|=2$ y \( \alpha=45^\circ\)
Módulo 3 y argumento \(-30^\circ \)
$\left|\vec{u}\right|=1$ y \( \alpha=5\pi/4 \;rad\)
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0