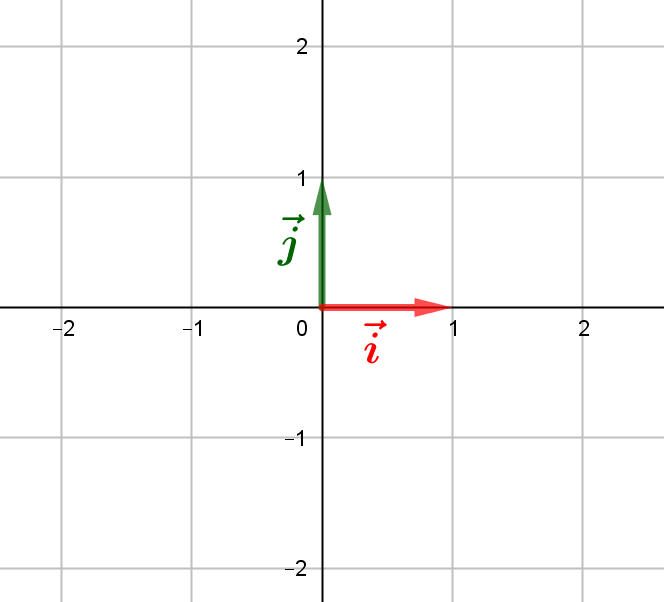
Para trabajar con vectores vamos a fijar un sistema de coordenadas: un origen, \((0,0) \), con dos ejes perpendiculares divididos en unidades horizontales, \(\vec{i} \) y verticales, \(\vec{j} \)

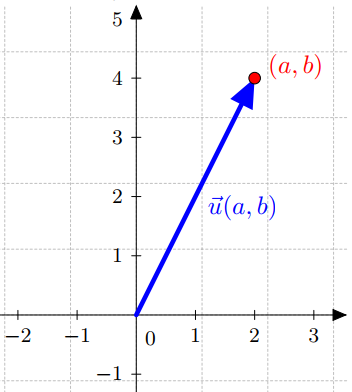
Así, cualquier vector, queda determinado por dos números, llamadas componentes del vector, \((x,y) \), la componente horizontal y la componente vertical.

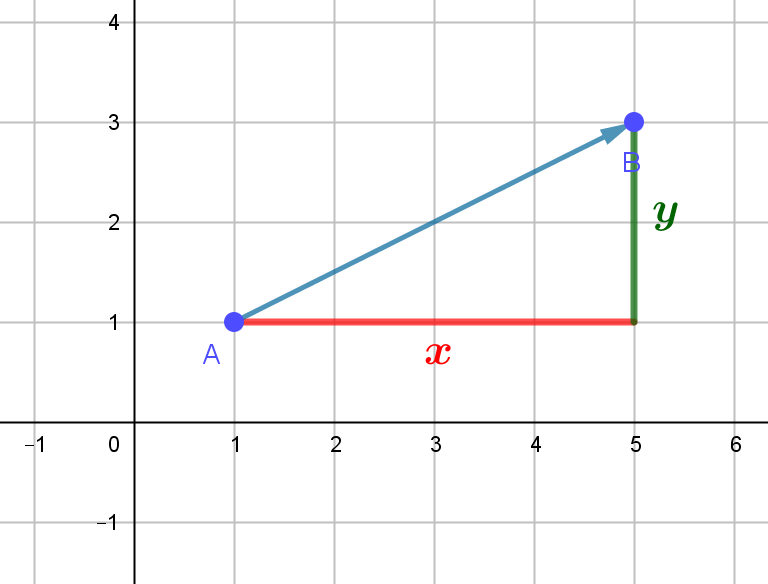
Escribiremos el vector como $\vec{AB}=\left(x,y\right)$ y diremos que $x$ es la componente horizontal e $y$ la componente vertical del vector $\vec{AB}$.

Para calcular las componentes de un vector fijo $\vec{AB}$ restamos las coordenadas del extremo, $B$, menos las del origen $A$.

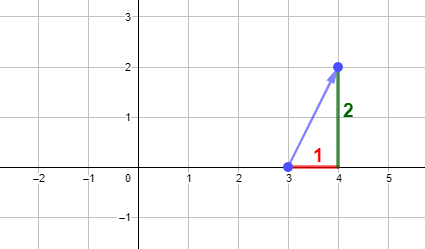
En este ejemplo podemos ver que las componentes del vector \(\vec{AB} \) son \((4,2)=4\vec{i}+2\vec{j} \)

En Fisica se utiliza más la segunda notación que la primera. En nuestro trabajo sobreentenderemos que nuestro sistema de coordenadas es \({(0,0),\vec{i},\vec{j}} \) y simplificaremos la expresión en coordenadas de un vector escribiendo directamente \((x,y) \).