Derivabilidad y continuidad
Por analogía con el concepto de límite por la izquierda y por la derecha de una función, definimos los conceptos de derivada lateral por la izquierda y por la derecha de una función en un punto.
La derivada lateral por la izquierda de la función $y=f(x)$ en el punto $x=a$, la denotamos por $f'(a)$ y se calcula:
$f'(a^-)=\lim_{x\to 0^-}{\dfrac{f(a+h)-f(a)}{h}}$
La derivada lateral por la derecha de la función $y=f(x)$ en el punto $x=a$, la denotamos por $f'(a^+)$
$f'(a^+)=\lim_{x\to 0^+}{\dfrac{f(a+h)-f(a)}{h}}$$
Para que una función sea derivable en un punto tiene que suceder:
-
Que la función sea continua.
-
Que existan las derivadas laterales y estas sean iguales, es decir, que la función derivada sea una función continua.
Una función derivable en un punto es también continua en ese punto. El recíproco no es cierto, es decir, una función continua en un punto no tiene por qué ser derivable en ese punto.
Para estudiar la derivabilidad en un punto, en un función definida a trozos, primero hemos de estudiar la continuidad y después la derivabilidad.
En un gráfica donde exista un "pico" podemos decir que la función no es derivable, es decir, la derivada mide la suavidad de la función.
Ejemplo
Estudia la derivabilidad de la función
$f(x)=\begin{cases} x^{2}+1 & x\leq0 \\ e^{x} & x>0 \end{cases} $
Primero estudiamos la continuidad:
Las dos funciones son continuas en sus dominios, la primera por ser un polinomio y la segunda por ser una exponencial. El único punto donde tenemos que estudiar la continuidad es en el punto donde se empalman las dos funciones, es decir, $x=0$:
-
$\lim_{x\to 0^-}{(x^2+1)}=1$
-
$\lim_{x\to 0^+}{e^x}=1$
-
$f(0)=1$
Por tanto, la función es continua en todo $\mathbb{R}$.
Estudiamos ahora la derivabilidad en $x=0$:
Podemos hacer las derivadas de las dos funciones en todos los puntos salvo en $x=0$ porque no sabemos si ahí es derivable:
$f(x)=\begin{cases} 2x & x<0 \\ e^{x} & x>0 \end{cases} $
Observa que hemos quitado el signo igual al hacer la derivada porque ahí no sabemos si es derivable.
Hallamos las derivadas laterales en $x=0$:
-
$f'(0^-)=2\cdot 0=0$
-
$f'(0^+)=e^0=1$
Las derivadas laterales no coinciden, por tanto, la función no es derivable en $x=0$.
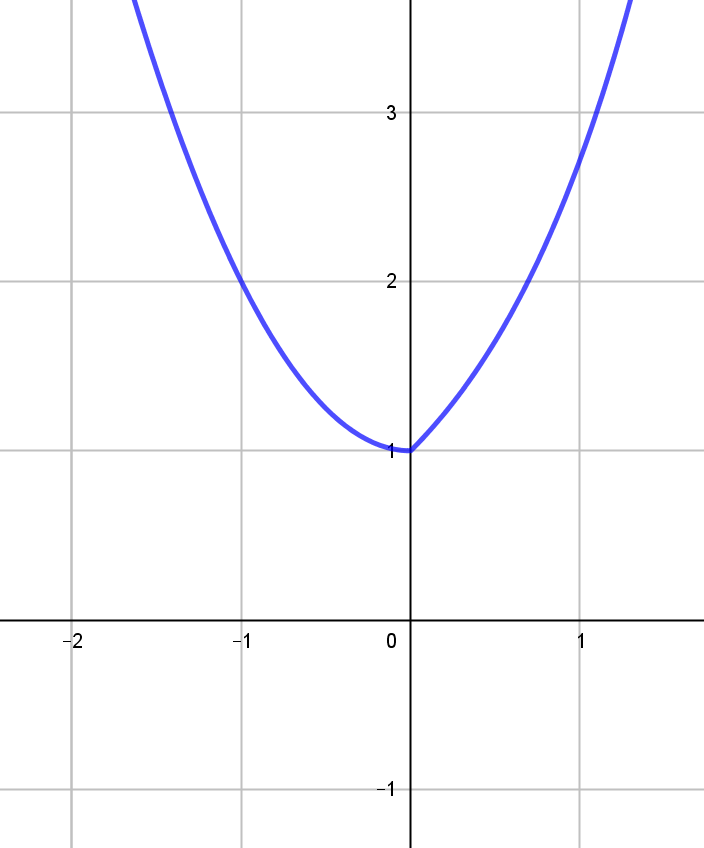
Esta es la gráfica de la función. Observa que en $x=0$ la función tiene un "pico", no es suave.
Ejercicios
1. Halla los valores de $a$ y $b$ para que la siguiente función sea derivable:
$f(x)=\begin{cases} ax^{2}+1 & x\leq1 \\ x^2+bx+3 & x>1 \end{cases} $
2. Halla $a$ y $b$ para que la siguiente función sea derivable:
$f(x)=\begin{cases} \sin x & x\leq0 \\ ax+b & x>0 \end{cases} $
Obra publicada con Licencia Creative Commons Reconocimiento No comercial Compartir igual 4.0