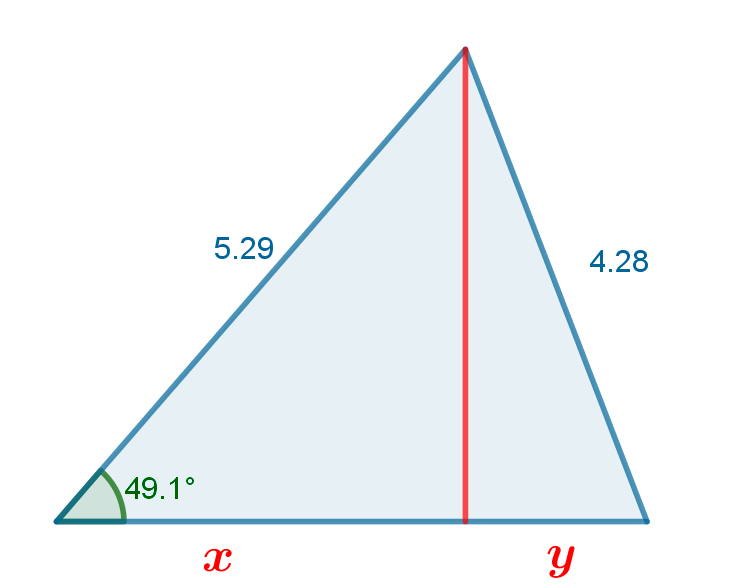
Resolver un triángulo es calcular los tres ángulos y las longitudes de los tres lados del triángulo.
Si el triángulo es rectángulo se nos pueden dar tres casos:
Caso 1
Se conocen dos lados
Utilizaremos el Teorema de Pitágoras para conocer el tercer lado. Para conocer los ángulos del triángulo podremos utilizar cualquiera de las tres razones trigonométricas principales: seno, coseno o tangente.
Caso 2
Se conocen un ángulo agudo y la hipotenusa
El otro ángulo agudo lo sacamos porque la suma de los dos ángulos agudos ha de ser $90^\circ$. Podemos aplicar la definición del seno o del coseno en cualquiera de los dos ángulos para calcular los dos catetos.
Caso 3
Se conocen un ángulo agudo y un cateto
El otro ángulo agudo lo sacamos porque la suma de los dos ángulos agudos ha de ser $90^\circ$. Podemos aplicar la definición del seno, del coseno o de la tangente en cualquiera de los dos ángulos para calcular la hipotenusa y el otro cateto.