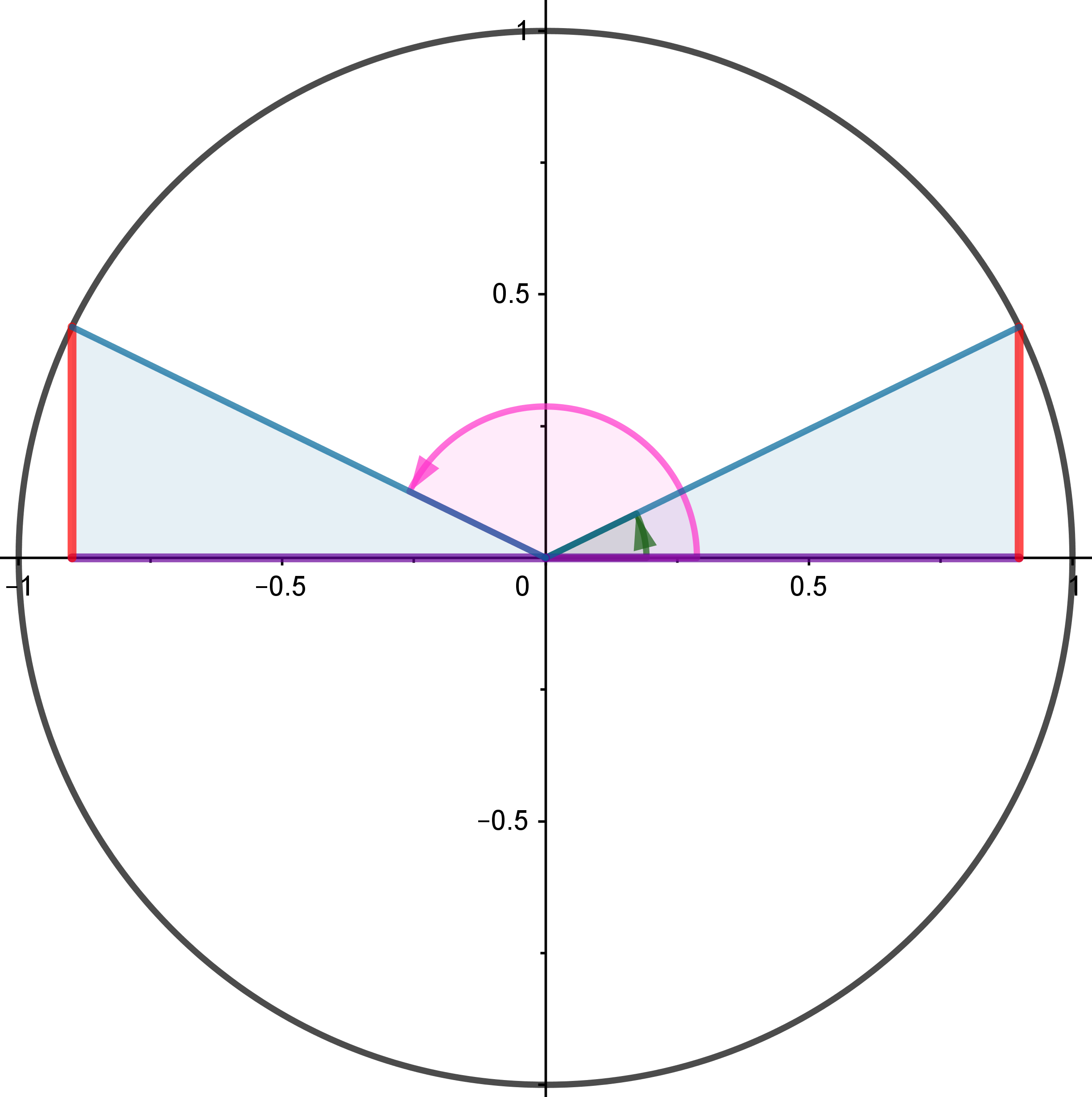
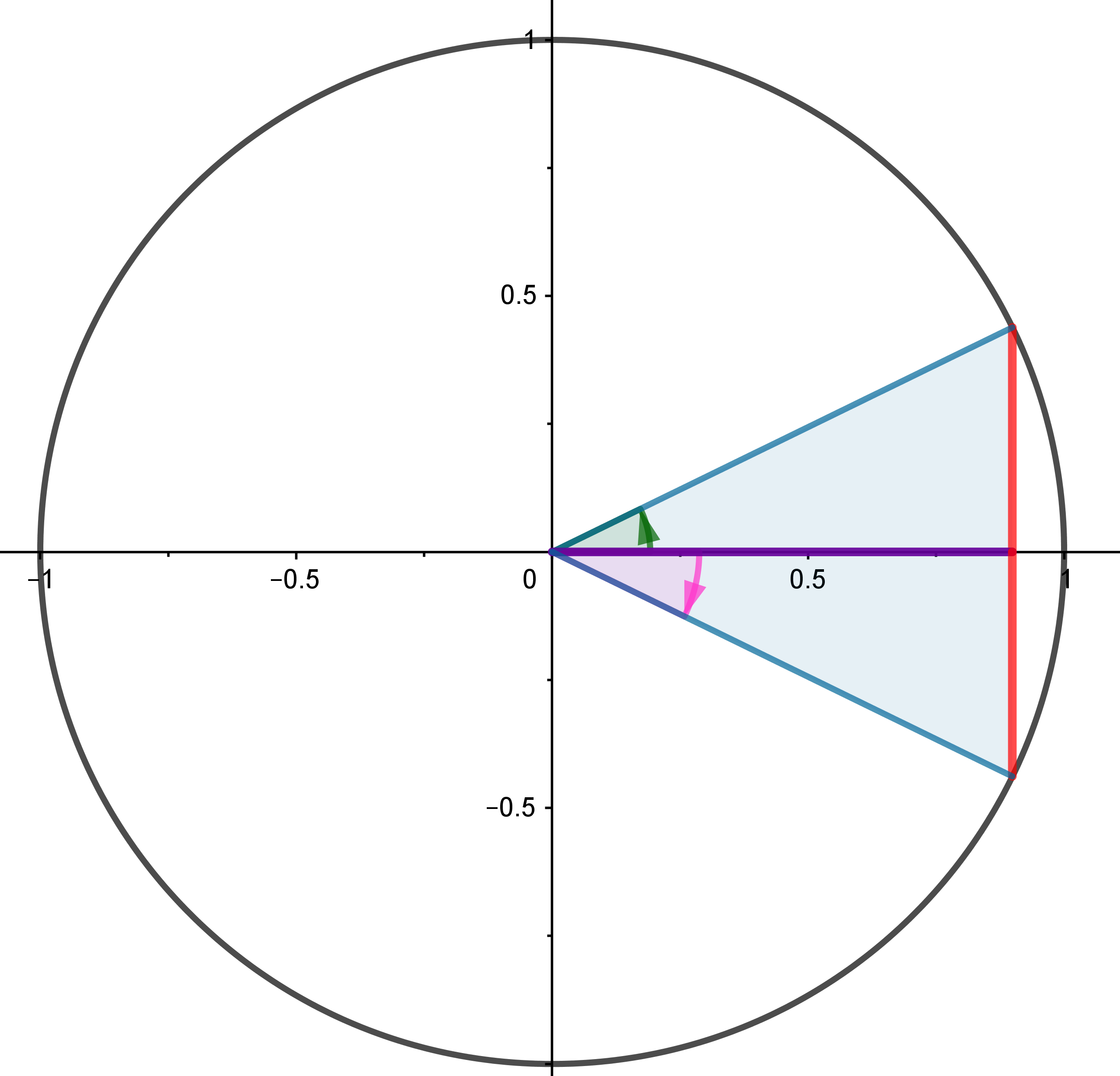
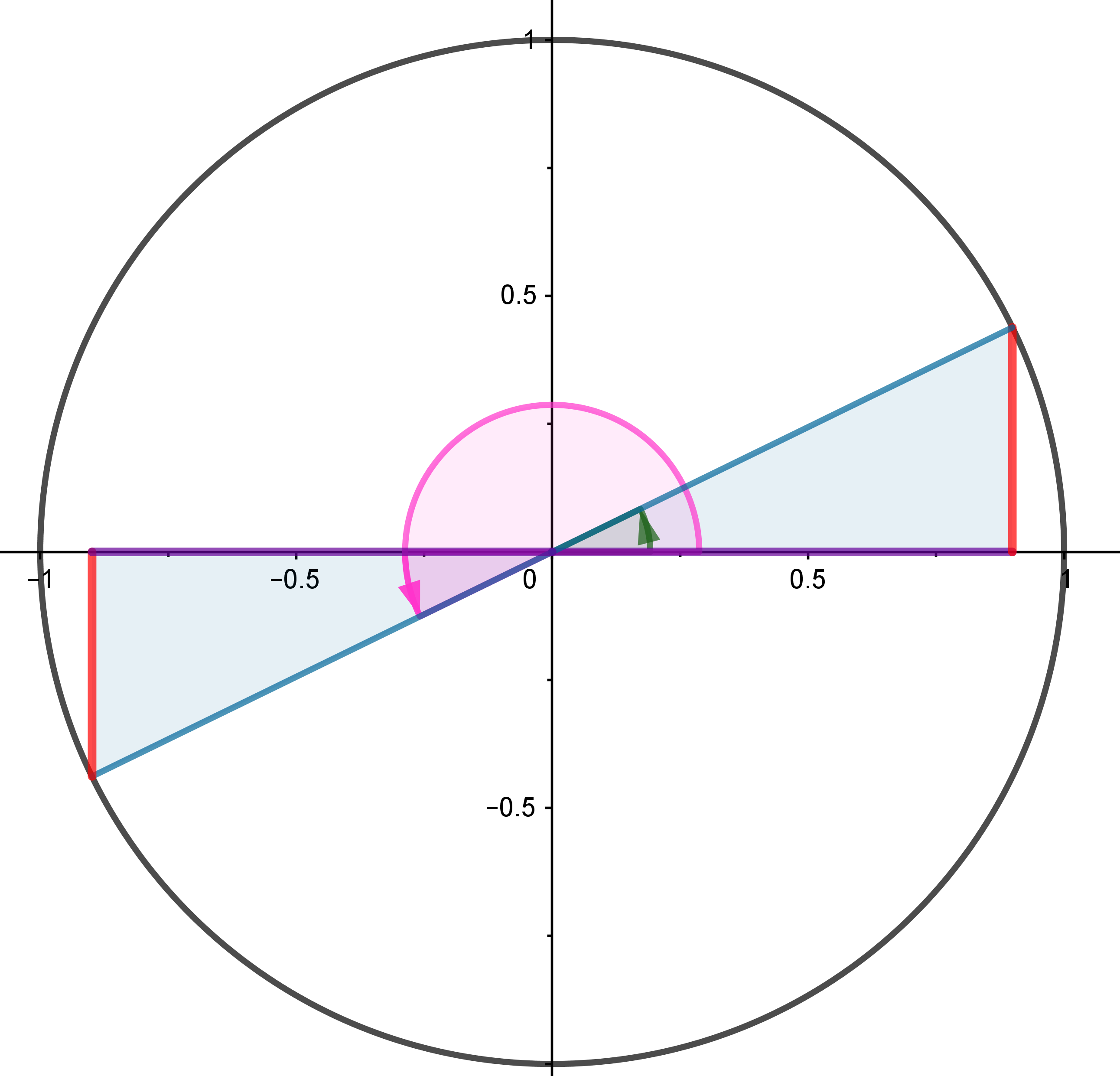
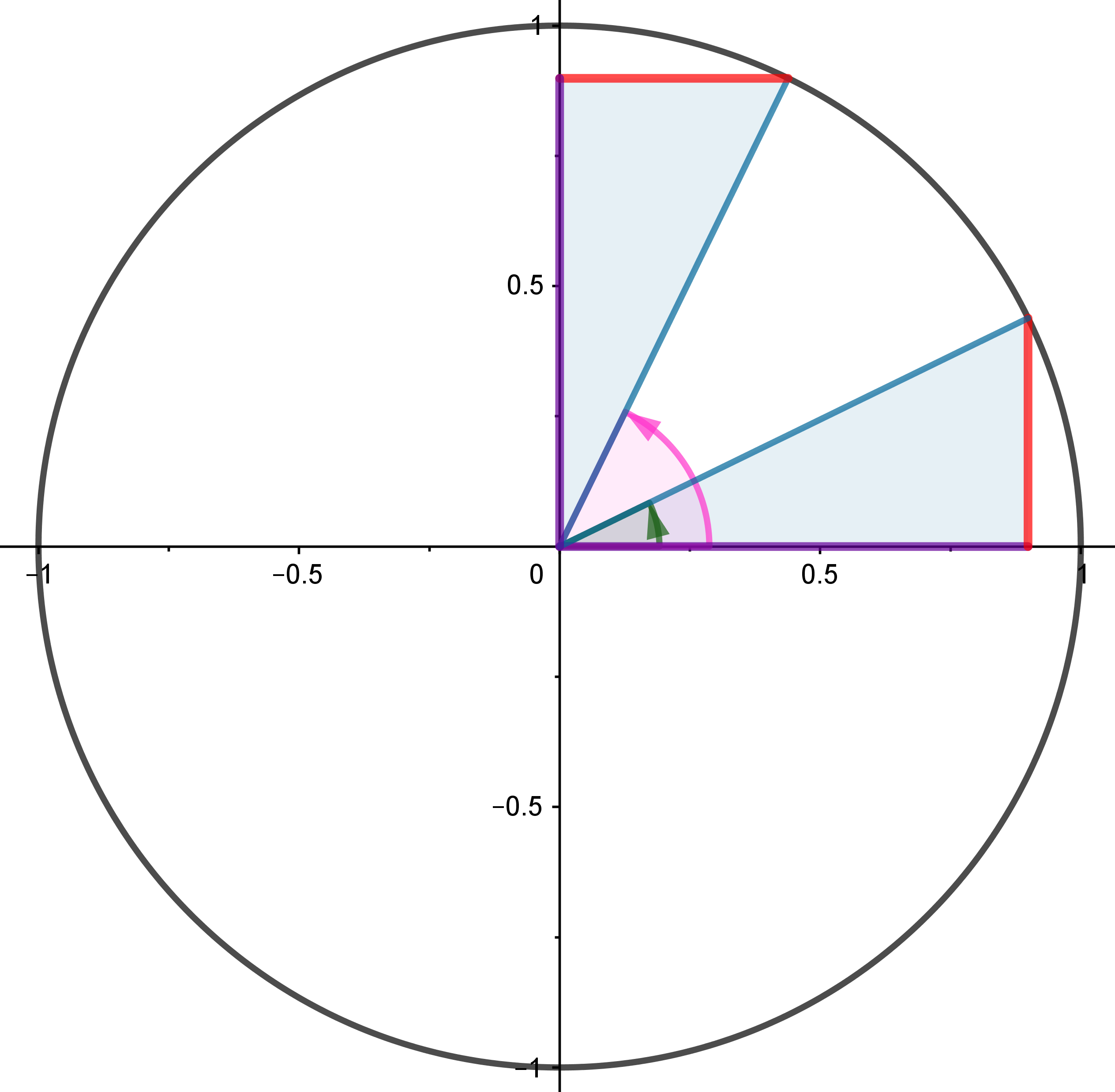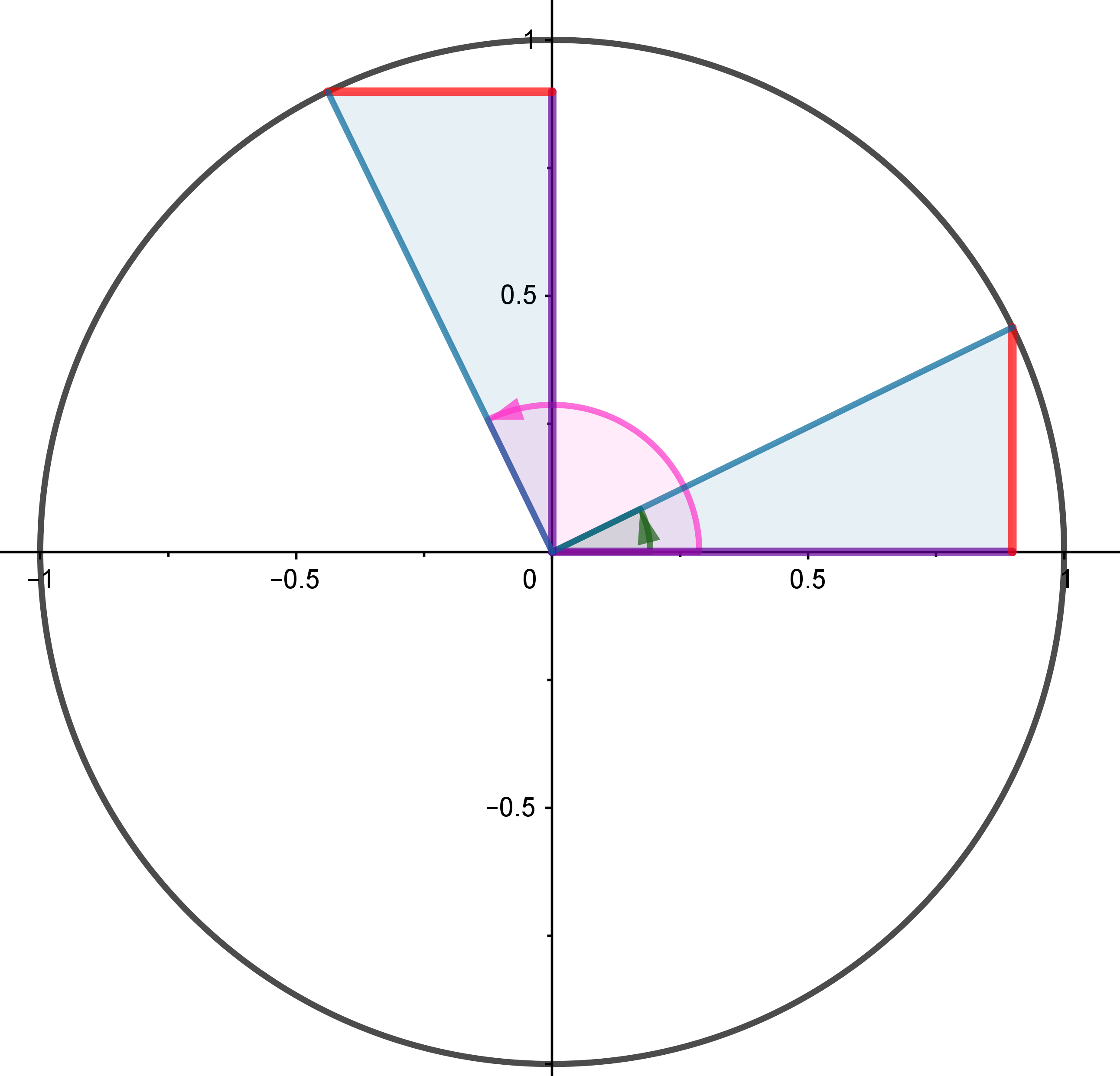Saltar la navegación

Reducción de razones al primer cuadrante

Entre las razones trigonométricas de ángulos complementarios, suplementarios, opuestos y que se diferencian en uno y dos rectos se establecen ciertas relaciones interesantes de estudiar.

Será especialmente importante cuando queramos calcular con la calculadora, qué ángulos corresponden a una cierta razón trigonométrica. La calculadora sólo nos va a devolver un valor y sin embargo existen infinitos ángulos que tienen esa razón trigonométrica. En la mayoría de los casos, son dos las soluciones en la primera vuelta a la circunferencia.

Relación entre ángulos complementarios

Recordamos que dos ángulos son complementarios cuando al sumarlos obtenemos un ángulo recto. Sean $\alpha$ y $\beta=90^\circ-\alpha$ dos ángulos complementarios.

Razones entre ángulos complementarios

  • $\sin(\beta)=\sin(90^\circ-\alpha)=\cos\alpha$

  • $\cos(\beta)=\cos(90^\circ-\alpha)=\sin\alpha$

  • $\tan(\beta)=\tan(90^\circ-\alpha)=\dfrac{\cos\alpha}{\sin\alpha}=\cot\alpha$

Relación entre ángulos suplementarios

Recordamos que dos ángulos son suplementarios cuando al sumarlos obtenemos un ángulo llano. Sean $\alpha$ y $\beta=180^\circ-\alpha$ dos ángulos suplementarios.

Razones suplementarios

  • $\sin(\beta)=\sin(180^\circ-\alpha)=\sin\alpha$

  • $\cos(\beta)=\cos(180^\circ-\alpha)=-\cos\alpha$

  • $\tan(\beta)=\tan(180^\circ-\alpha)=\dfrac{\sin\alpha}{-\cos\alpha}=-\tan\alpha$

Relación entre ángulos opuestos

$\alpha$ (sentido antihorario) y $\beta=-\alpha$ (sentido horario) son ángulos opuestos porque al sumarlos obtenemos $360^\circ$.

Razones ángulos opuestos

  • $\sin(\beta)=\sin(-\alpha)=-\sin\alpha$

  • $\cos(\beta)=\cos(-\alpha)=\cos\alpha$

  • $\tan(\beta)=\tan(-\alpha)=\dfrac{-\sin\alpha}{\cos\alpha}=-\tan\alpha$

Relación entre ángulos que se diferencian en un recto

Sean los ángulos $\alpha$ y $\beta=90^\circ+\alpha$:

Razones ángulos difieren 90

  • $\sin(\beta)=\sin(90^\circ+\alpha)=\cos\alpha$

  • $\cos(\beta)=\cos(90^\circ+\alpha)=-\sin\alpha$

  • $\tan(\beta)=\tan(90^\circ+\alpha)=\dfrac{\cos\alpha}{-\sin\alpha}=-\cot\alpha$

Relación entre ángulos que se diferencian en dos rectos

Sean los ángulos $\alpha$ y $\beta=180^\circ+\alpha$:

Razones ángulos difieren 180

  • $\sin(\beta)=\sin(180^\circ+\alpha)=-\sin\alpha$

  • $\cos(\beta)=\cos(180^\circ+\alpha)=-\cos\alpha$

  • $\tan(\beta)=\tan(180^\circ+\alpha)=\dfrac{-\sin\alpha}{-\cos\alpha}=\tan\alpha$

Conclusión importante

  • Los ángulos que tienen el mismo seno son suplementarios, es decir, suman entre los dos $180^\circ$

  • Los ángulos que tienen el mismo coseno son opuestos.

  • Los ángulos que tienen la misma tangente difieren en $180^\circ$.

Ejercicio 1

Encuentra todos los ángulos menores de $360^\circ$ que cumplen:

  1. Que el seno es igual a 0,5.

  2. Que el coseno es igual a $\sqrt{3}/2$.

  3. Que la tangente es igual a 1,3.

  4. Que el seno valga 0.

  5. Que el coseno valga 0.

Ejercicio 2

Encuentra todos los ángulos  que cumplen:

  1. Que el seno es igual a $\sqrt{2}/2$.

  2. Que el coseno es igual a $1/2$.

  3. Que la tangente es igual a 0,8653.

Ejercicio 3

Sin utilizar la calculadora,  halla las razones trigonométricas de los siguientes ángulos reduciéndolas a uno del primer cuadrante conocido.

  • $150^\circ$

  • $5\pi/4\,rad$

  • $-60^\circ$

  • $120^\circ$

  • $315^\circ$

Te puedes apoyar en la siguiente escena de GeoGebra para encontrar los ángulos del primer cuadrante que necesitas.

Creado con eXeLearning (Ventana nueva)