Has ahora sólo hemos definido las razones trigonométricas para ángulos agudos, pero, ¿cómo se amplían las definiciones del seno, coseno o tangente para ángulos mayores de $90^{\circ}$?

Para ampliar sus definiciones nos vamos a ayudar de la circunferencia goniométrica.

Llamamos circunferencia goniométrica a una circunferencia de radio 1 y centro en el eje de coordenadas. Nos va a ser útil para ampliar las razones trigonométricas a cualquier ángulo.

Podemos dividir la circunferencia goniométrica en cuatro cuadrantes:

En la siguiente escena puedes ver tanto en grados como en radianes los ángulos que nos salen con más asiduidad al trabajar con las razones trigonométricas.

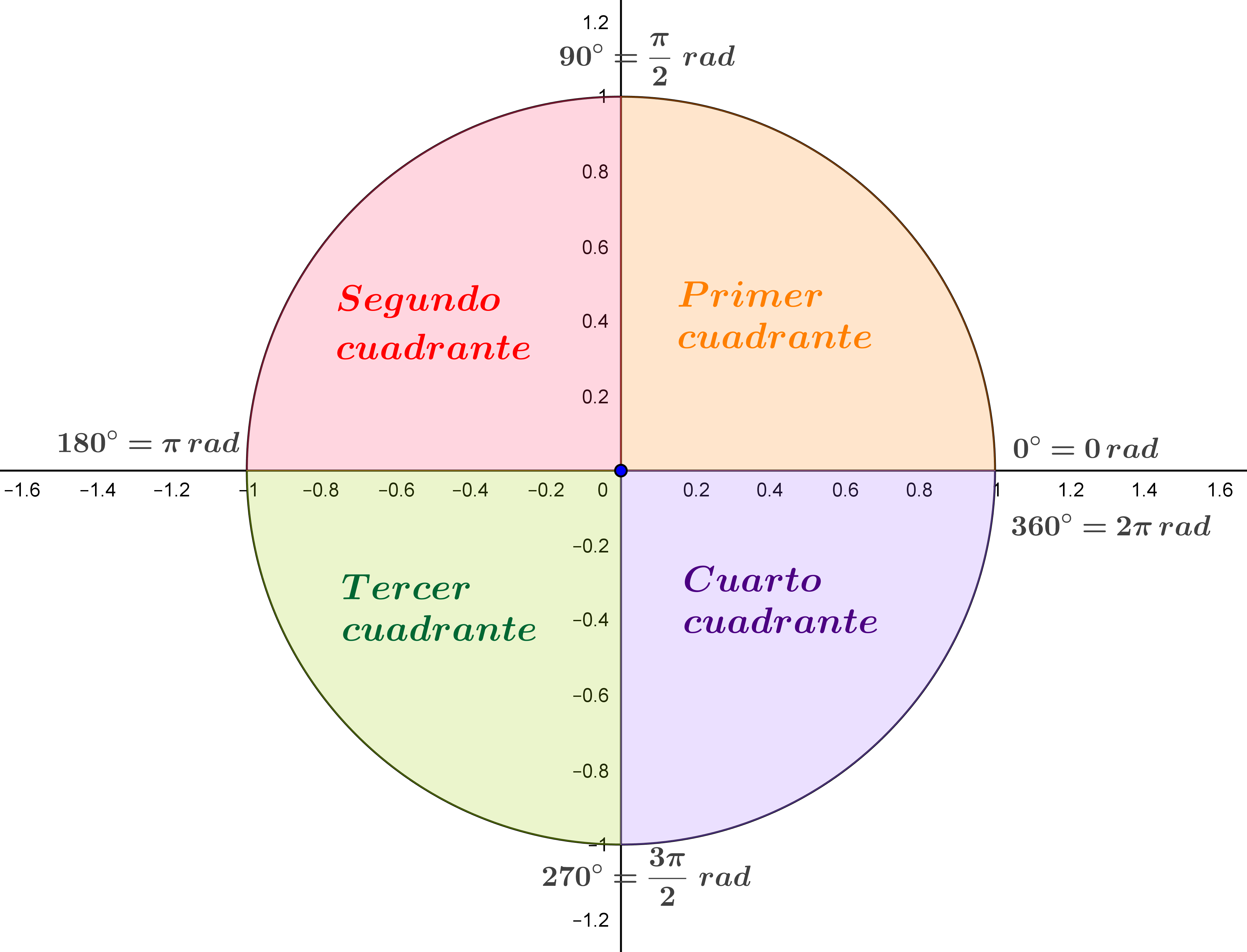
La circunferencia goniométrica tiene radio 1. Para cualquier triángulo rectángulo en el que uno de sus vértices sea el centro de la circunferencia y el vértice correspondiente a la hipotenusa se encuentre sobre la hipotenusa se tiene que la hipotenusa (radio de la circunferencia) vale 1.

Observa la siguiente escena y mueve el punto $C$ a lo largo del primer cuadrante.

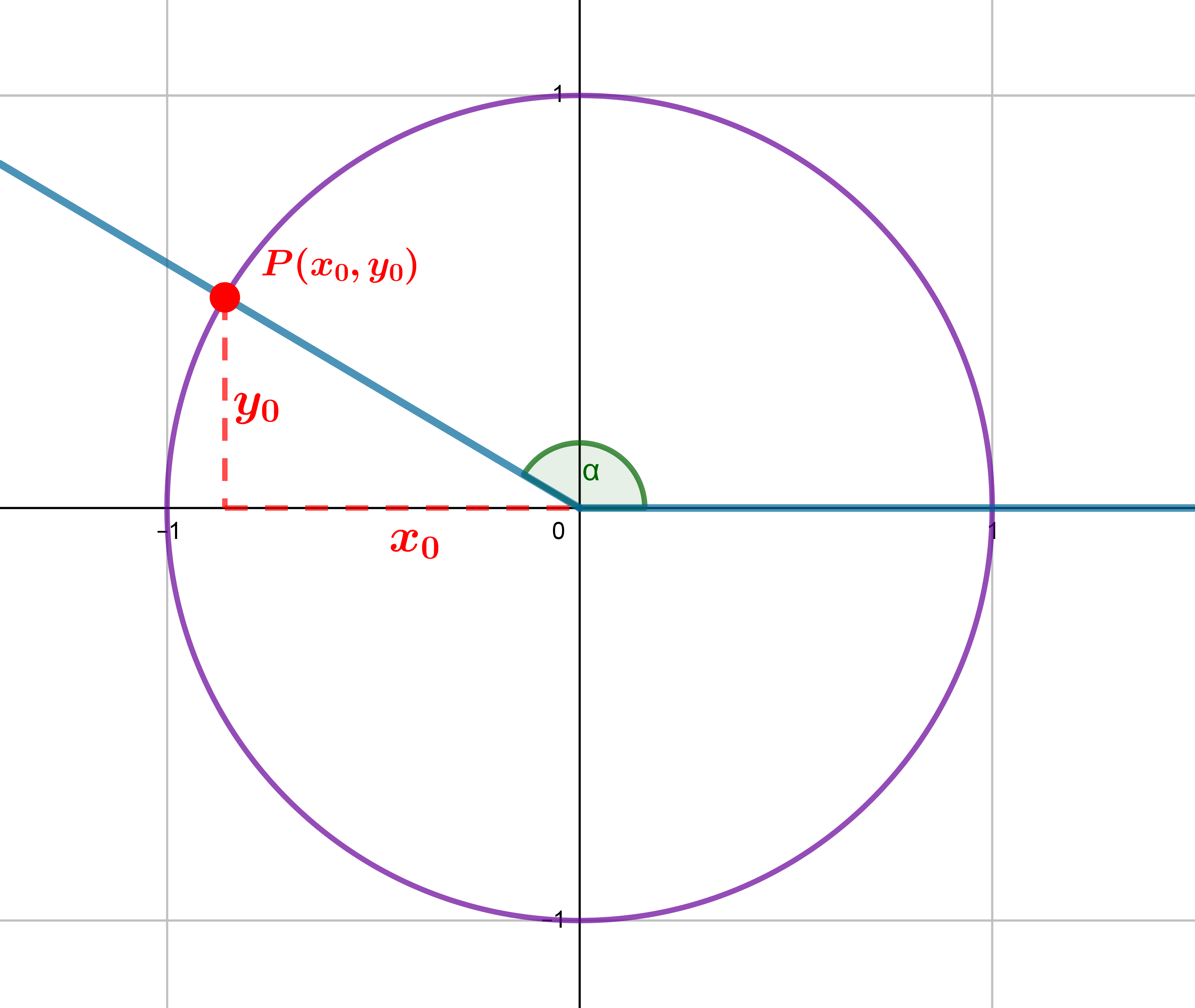
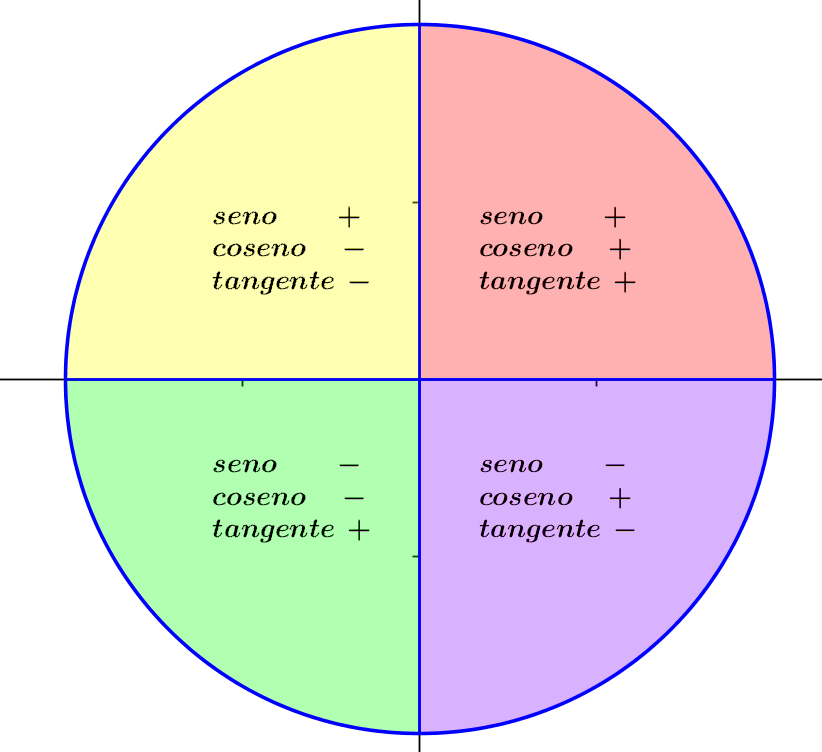
En la circunferencia goniométrica se ve claramente como el seno del ángulo coincide con el cateto opuesto y es la ordenada del punto $C$, el coseno del ángulo coincide con el cateto contiguo y la abscisa del punto $C$. La tangente es la longitud del segmento $B'C'$.

¿Puedes explicar por qué el valor de la tangente se corresponde con el segmento \(\overline{B'C'}\)

Ya estamos preparados para poder extender la definición de razones trigonométricas para ángulos mayores de $90^{\circ}$, es decir, del segundo, tercer y cuarto cuadrante.

En todos los casos, el seno va a ser el valor de la ordenada y el coseno el valor de la abscisa del punto de la circunferencia que determina la semirrecta que define el ángulo, pero teniendo en cuenta los signos:

• Las abscisas, las $x$, el coseno, es positivo en el primer y cuarto cuadrante (hacia la derecha).

• Las ordenadas, las $y$, el seno, es positivo en el primer y segundo cuadrante (hacia arriba).

Los signos de la tangente se deducen de la regla de los signos puesto que $\tan\alpha=\dfrac{\sin\alpha}{\cos\alpha}$

Se puede entender que un ángulo mayor de $360^{\circ}$ tiene su equivalente a un ángulo entre $0^{\circ}$ y $360^{\circ}$ si pensamos que el primer ángulo es el resultado de dar más de una vuelta a la circunferencia.

Las razones trigonométricas de un ángulo mayor de $360^{\circ}$ son las mismas que otro ángulo que se diferencia del primero en un número determinado de vueltas a la circunferencia.

Las razones trigonométricas, del ángulo $\alpha=360^{\circ}$ son las mismas que las del ángulo de $30^{\circ}$ porque $390^{\circ}$ es dar una vuelta completa a la circunferencia más $30^{\circ}$.

$390=360\cdot 1+30$