Razones trigonométricas para ángulos agudos
Recuerda que en Matemáticas, una razón, es un cociente entre dos cantidades. Por tanto, las razones trigonométricas van a definirse como ciertos cocientes.
Dado un triángulo rectángulo con ángulos agudos $\alpha$ y $\beta$
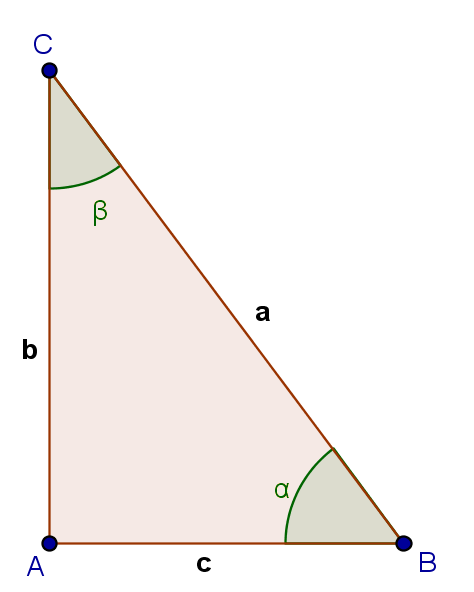
Se definen las siguientes razones trigonométricas:
Seno del ángulo $\alpha$
El seno del angulo $\alpha$ es el cociente entre el cateto opuesto al ángulo $\alpha$ y la hipotenusa.
$\sin\alpha=\frac{b}{a}$
El coseno del angulo $\alpha$
El coseno del angulo $\alpha$ es el cociente entre el cateto contiguo al ángulo $\alpha$ y la hipotenusa.
$\cos\alpha=\dfrac{c}{a}$
La tangente del ángulo $\alpha$
La tangente del ángulo $\alpha$ es el cociente entre el cateto opuesto y el cateto contiguo al ángulo $\alpha$.
$\tan\alpha=\dfrac{b}{c}$
La cosecante del ángulo $\alpha$
La cosecante del ángulo $\alpha$ es la razón inversa al seno de $\alpha$.
$\text{cosec} \alpha=\dfrac{1}{\sin\alpha}=\dfrac{a}{b}$
La secante del ángulo $\alpha$
La secante del ángulo $\alpha$ es la razón inversa al coseno de $\alpha$.
$\sec\alpha=\dfrac{1}{\cos\alpha}=\dfrac{a}{c}$
La cotangente del ángulo $\alpha$
La cotangente del ángulo $\alpha$ es la razón inversa de la tangente de $\alpha$.
$\cot\alpha=\dfrac{1}{\tan\alpha}=\dfrac{c}{b}$
y suele estar encima de la tecla 
y suele estar encima de la tecla 
y suele estar encima de la tecla 
