Las razones trigonométricas están relacionadas entre ellas, de tal modo, que con conocer una de ellas podemos hallar las otras dos. De entre las muchas relaciones que existen entre ellas (identidades trigonométricas) destacamos tres relaciones fundamentales.
Primera relación fundamental
$\sin^2 x+\cos^2 x=1$
Demostración:
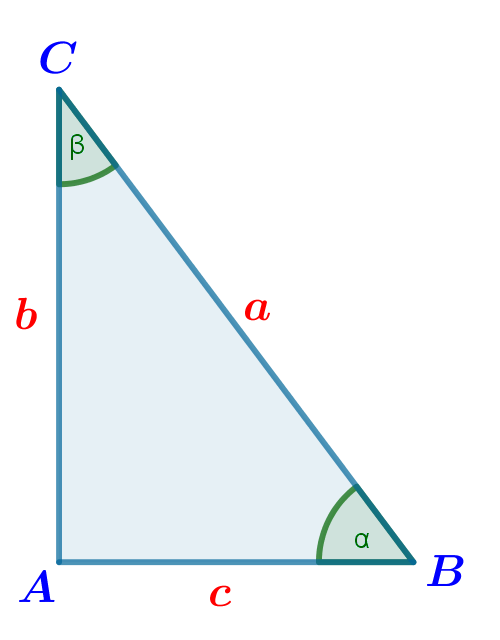
$\sin^{2}\alpha+\cos^{2}\alpha=\left(\dfrac{b}{a}\right)^{2}+\left(\dfrac{c}{a}\right)^{2}=\dfrac{b^{2}}{a^{2}}+\dfrac{c^{2}}{a^{2}}=\dfrac{b^{2}+c^{2}}{a^{2}}\overset{*}{=}\dfrac{a^{2}}{a^{2}}=1$
{*} Aplicamos el teorema de Pitágoras: $a^{2}=b^{2}+c^{2}$.
Segunda relación fundamental
$\tan x=\dfrac{\sin x}{\cos x}$
Demostración:
Aplicamos las definiciones de las razones trigonométricas:
$\dfrac{\sin\alpha}{\cos\alpha}=\dfrac{\frac{b}{a}}{\frac{c}{a}}=\dfrac{b}{c}=\tan\alpha$
Tercera relación fundamental
$1+\tan^{2}\alpha=\dfrac{1}{\cos^{2}\alpha}$
Demostración:
Partimos del lado izquierdo de la igualdad:
$1+\tan^{2}\alpha=1+\left(\dfrac{b}{c}\right)^{2}=1+\dfrac{b^{2}}{c^{2}}=\dfrac{c^{2}+b^{2}}{c^{2}}\overset{*}{=}\dfrac{a^{2}}{c^{2}}=\dfrac{1}{\left(\frac{c^{2}}{a^{2}}\right)}=\dfrac{1}{\cos^{2}\alpha}$
{*} Aplicamos el teorema de Pitágoras: $a^{2}=b^{2}+c^{2}$