Función Inversa
Dada una función $y=f(x)$, se llama función inversa de $f$ y se denota por $f^{-1}$ a otra función que para cualquier valor del dominio de $f$ se cumple que:
-
$(f\circ f^{-1})(x)=x$
-
$(f^{-1}\circ f)(x)=x$
No todas las funciones tienen inversa, para que exista se tiene que cumplir que cada valor del recorrido de $f$, $y$, proviene de un único valor del dominio, $x$. A este tipo de funciones, las llamaremos funciones inyectivas.
La función $y=x^2$ no tiene inversa porque cada valor del recorrido (excepto el cero) proviene de dos valores del dominio. Por ejemplo, el 4, es imagen de 2 y -2: $f(2)=4$ y $f(-2)=4$.
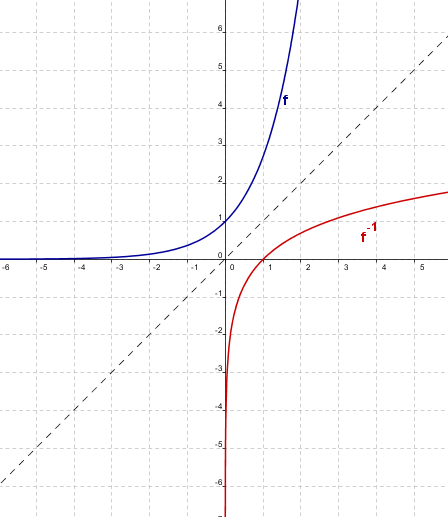
Las gráficas de una función y su inversa son simétricas con respecto a la recta $y=x$
Cálculo de la función inversa
En la práctica, para hallar la función inversa de una función $y=f(x)$ se intercambian los nombres de $x$ e $y$ y se despeja la variable $y$
Ejemplo
Calcula la inversa de la función $f(x)=3x-2$.
Primero intercambiamos las variables $x$ e $y$:
$$x=3y-2$$
Despejamos la $y$:
$$\begin{array}{ccc} x & = & 3y-2 \\ 3y & = & x+2 \\ y & = & \frac{x+2}{3} \end{array}$$
Por tanto, la función inversa de $f(x)=3x-2$ es $f^{-1}=\dfrac{x+2}{3}$.
Vamos a comprobar que efectivamente es la inversa:
-
$(f\circ f^{-1})(x)=f \left( f^{-1}(x) \right)=f \left( \dfrac{x+2}{3} \right)=3\cdot \dfrac{x+2}{3}-2=x$
-
$(f^{-1} \circ f)(x)=f^{-1} \left( f(x) \right)=f^{-1}(3x-2)=\dfrac{3x-2+2}{3}=x$
Ejercicios
Comprueba que las funciones $f(x)=\sqrt{x+4}$ y $g(x)=x^2-4$ son inversas.
Calcula la inversa de las funciones:
-
$y=-2x+3$
-
$y=\dfrac{2x-1}{x+3}$
Obra publicada con Licencia Creative Commons Reconocimiento 4.0