Saltar la navegación

Dominio y Recorrido

Definiciones

Dominio

Dada una función, $y=f(x)$, se llama dominio de la función $f$ al conjunto de los números para los que está definida la función.

Es el conjunto de valores que toma la variable independiente, $x$.

Recorrido

Dada una función $y=f(x)$, se llama recorrido o imagen de la función $f$ al conjunto de valores que toma la variable dependiente $y$, es decir, el conjunto de los números $y$ que provienen de algún $x$.

Si tenemos una función que asigna a cada número su cuadrado, el dominio serán todos los números porque puedo calcular el cuadrado de cualquier número, sin embargo, la imagen son los números a partir del cero porque no existe ningún número que al elevarlo al cuadrado de un número negativo:

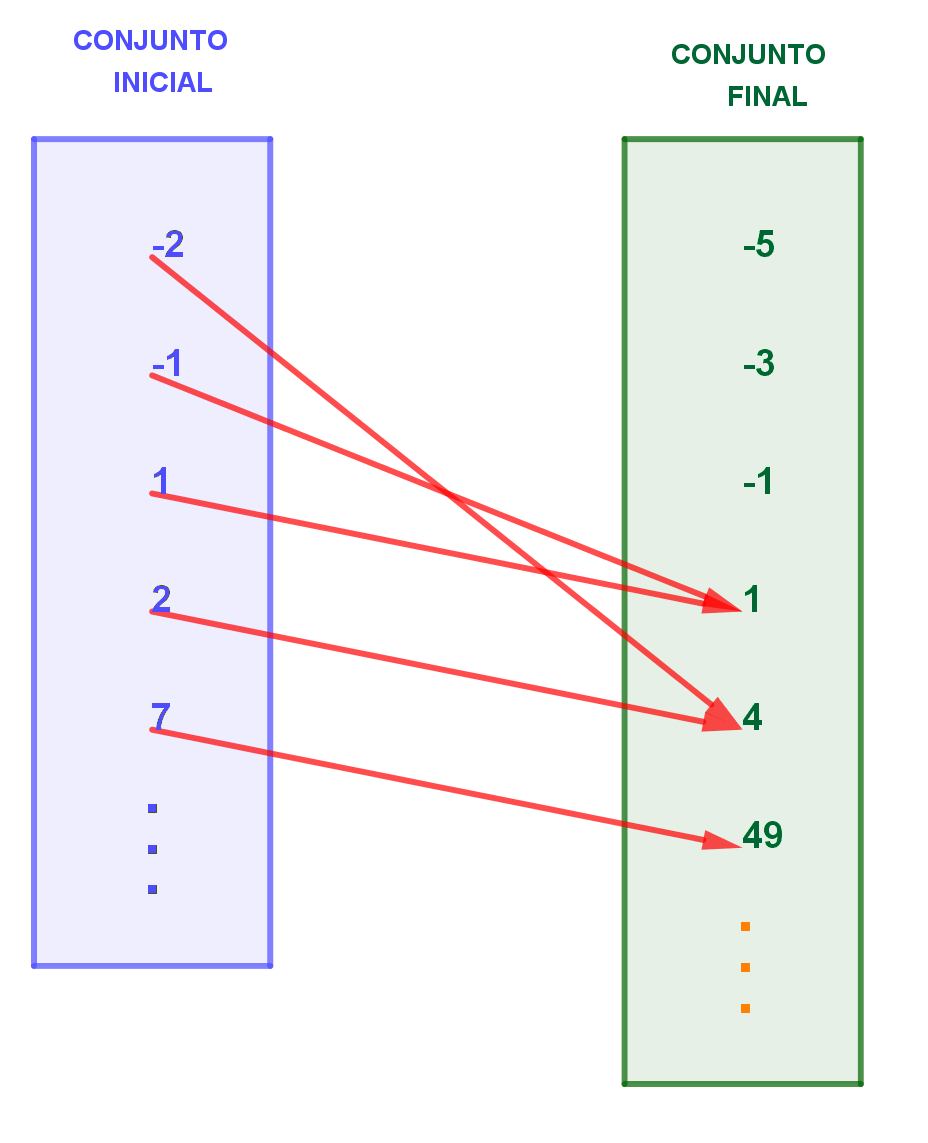
Como se puede ver en la imagen anterior, el -5 no proviene ni puede provenir de ningún elemento del conjunto inicial, ¿qué número al elevarlo al cuadrado da como resultado -5? Ninguno.

Dominio y recorrido de una función dada su gráfica

En el siguiente applet vemos como se calcula el dominio y el recorrido de una función dada su gráfica.

  • Para calcular el dominio marca la casilla Dominio y desliza el punto A sobre el eje X (eje de abscisas). El dominio lo formarán todos los puntos de dicho eje que tienen imagen por $f$. En el texto verde aparece la imagen del punto A lo que significa que el punto $(A,f(A))$ pertenece a la gráfica de la función.
  • Para calcular el recorrido marca la casilla Recorrido y desliza el punto C sobre el eje Y (eje de ordenadas). C pertenecerá al recorrido o imagen cuando la recta perpendicular al eje Y que pasa por C intersece con la función.

En este ejemplo, el dominio está formado por todos los números salvo el $-2$ y el $2$. La imagen está formada por todos los números negativos hasta el cero, incluido, y por los números desde el 1 hasta el  $\infty$, pero sin incluir el $1$.

Dominio de función dada su expresión algebraica

En general, el dominio de las funciones es toda la recta real, $\mathbb{R}$, con las siguientes excepciones:

a) En las funciones racionales hay que excluir los puntos en los que el denominador vale 0, porque no se puede dividir por cero.

b) En las funciones irracionales con índice par, el radicando tiene que ser mayor o igual que cero, porque las raíces de índice par con radicando negativo no son números reales.

c) En las funciones logarítmicas el argumento tiene que ser positivo, porque el logaritmo de un número negativo o cero no existe en los números reales.

Ejemplo

Calcula el dominio de las siguientes funciones:

  1. $f(x)=\dfrac{x}{x^2-5x+6}$

    • El dominio es $Dom(f)=\mathbb{R}-\{2,3\}$ porque son los puntos donde se anula el denominador.

  2. $f(x)=\sqrt{x-2}$

    • El dominio de esta función es el intervalo $[2,+\infty)$ porque los valores de la raíz son positivos en ese intervalo.

  3. $f(x)=\log x+3$

    • El dominio de esta función es: $Dom(f)=\left(0,+\infty \right)$ porque el argumento del logaritmo no puede tomar valores negativos.