Estudio de las proporciones
Una proporción es una igualdad de dos razones:
\[\frac{a}{b}=\frac{c}{d},\,\,\text{con }b,c\neq0\]
Dado un rectángulo de lados \(a\) y \(b\), se define la proporción de un triángulo como:

\[p=\dfrac{max(a,b)}{min(a,b)}\]
¡Al contrario que las banderas!
Los matemáticos de la antigua Grecia dividieron los rectángulos en dos tipos: los rectángulos estáticos, que son aquellos en los que la proporción se puede poner en forma de fracción, es decir, en forma de razón de números enteros, y los rectángulos dinámicos, que son aquellos en los que no se puede poner en esa forma y, por tanto, su proporción es un número irracional.
-
\(\dfrac{a}{b}\in \mathbb{Q}\)
-
\(\dfrac{a}{b}\in \mathbb{I}\)
ESTÁTICAS
| Cuadrada | \(\dfrac{a}{b}=1\) |  |
|---|---|---|
| Dupla | \(\dfrac{a}{b}=2\) |  |
| Sesquilátera | \(\dfrac{a}{b}=\dfrac{3}{2}\) |  |
DINÁMICAS
| Raíz de dos | \(\dfrac{a}{b}=\sqrt{2}\) | 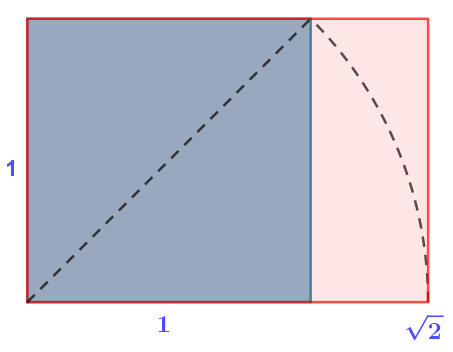 |
|---|---|---|
| Raíz de tres | \(\dfrac{a}{b}=\sqrt{3}\) | 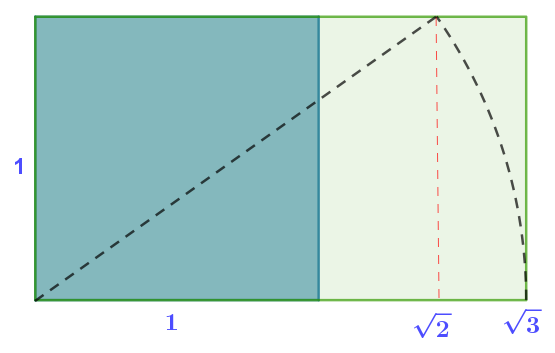 |
| Áurea | \(\dfrac{a}{b}=\dfrac{1+\sqrt{5}}{2}\) | 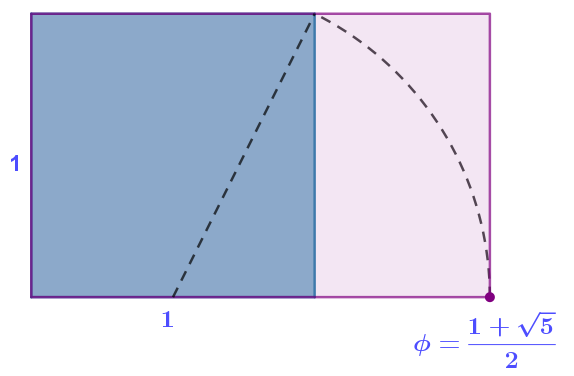 |