Demostración visual
En la siguiente actividad vamos a trabajar con el Teorema de Pitágoras. Es la demostración de dos maneras distintas
Áreas y perímetros 1º de la ESO
Sesión 9: Practicamos Teorema de Pitágoras
Otra demostración visual del Teorema de Pitágoras
https://www.geogebra.org/m/sfqu5r9r (Ventana nueva)
Hay cientos de demostraciones del Teorema de Pitágoras. Busca en Internet una demostración distinta a la que te ofrecemos aquí para presentársela a tus compañeros.
Problemas Teorema de Pitágoras con GeoGebra
Vamos a aprender a usar el Teorema de Pitágoras en problemas con enunciado. Pulsa en "Pista" para ir viendo los diferentes pasos de resolución de cada ejercicio.
Pulsando en "Otro Ejercicio", podremos ver datos y enunciados diferentes.
Desmarca la casilla "Modo aprendizaje" para obtener puntos por cada problema resuelto. Puedes seguir usando las pistas, pero obtendrás menos puntos.
https://www.geogebra.org/m/zXQDTAbB (Ventana nueva)
Creamos nuestro propio problema
Echa un vistazo al tipo de problemas que estamos resolviendo con el teorema de Pitágoras.
- ¿Hay alguna situación que te parezca interesante para recrearla? ¿Se te ocurre alguna nueva?
- Pues vamos a preparar una visualización "real" suya, y luego incluiremos nuestras explicaciones y cómo resolverla.
- Aquí lo importante no es que sea una situación muy novedosa sino ver la forma en que planteas el problema y usas el teorema de Pitágoras.
- Puedes hacer una construcción como la que te mostramos más abajo, o ¡salir a la calle a resolver los problemas matemáticos que encuentres!
- Toma fotografías para incluirlas con la actividad que presentes.
Practica
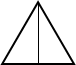
1. Sabiendo que el triángulo es equilátero y cada lado mide $6\,cm$, halla su altura.
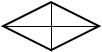
2. La diagonal mayor de este rombo mide 10 cm y la menor 6 cm. Halla el perímetro del rombo.
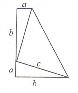
3. Esta figura mide 14 cm de alto y 10 cm de base. ¿Serías capaz de hallar su perímetro?
4. En el geoplano rodea con un hilo una pajarita como la de la figura y mide dicho hilo. Mide la distancia entre dos puntos consecutivos y, usando lo trabajado, comprueba si obtienes el mismo resultado.
5. En el portal de mi casa tengo este dibujo:
Los bordes de los rombos están desgastados y tengo que comprar una cinta negra fina para remarcarlos. Si el rectángulo mide 3,60 m de largo por 90 cm de alto, ¿cuánta cinta necesito?
6. El logo: Esta punta de flecha es el logotipo de una marca de coches. Si la queremos hacer con varitas de metal, calcula la longitud total de las mismas si el lado del cuadrado exterior mide 20 centímetros (el contorno pasa por el centro del cuadrado).
7. El botellero: En el botellero que hemos visto, (fíjate en la imagen) si el lado de un cuadradito mide 80 cm, ¿cuánto mide la diagonal? ¿Y si el área fuera \(0,81 m^2\)? Intenta resolver esto último sin hallar el lado del cuadradito.
8.
El velero: Este es mi barco de vela. Necesito comprar una vela nueva. Como puedes ver tiene forma de triángulo rectángulo y sé que la parte que va sujeta al mástil mide 5 metros. Si necesito reforzar la tela en los lados de la vela y ésta debe tener un área de 30 metros al cuadrado, ¿serías capaz de hallar cuanto mide el refuerzo que necesito?
9. Observa los cuadrados que hay dibujados en el suelo del parque situado en las cercanías de la iglesia de San Esteban de Salamanca. En cada dibujo hay tres cuadrados inscritos uno dentro del otro. Si el cuadrado mayor tiene de lado 1,20 m, ¿cuánto mide el área del cuadrado pequeño?
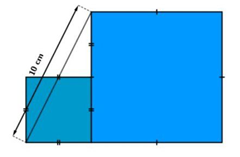
10. En la figura adjunta, ¿podrías calcular el área del cuadrado de la derecha?
Obra publicada con Licencia Creative Commons Reconocimiento Compartir igual 4.0