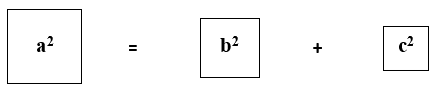Fíjate en este botellero. Es una trama con cuadrados y triángulos que podemos representar como la figura de al lado para trabajar con ella.

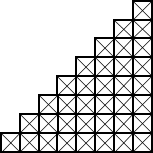
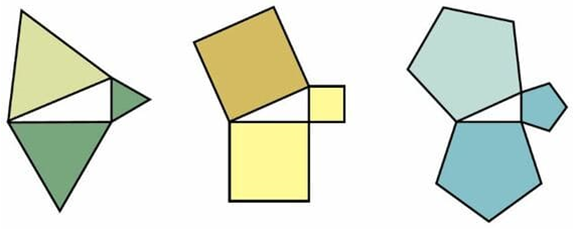
Resaltamos con otro color un triángulo rectángulo (hazlo mejor con uno que esté en el interior). Identifica los catetos y la hipotenusa. En cada uno de ellos, dibuja un cuadrado que tenga como lado en cada caso el cateto o la hipotenusa como hacemos en el ejemplo.

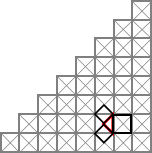
Estos cuadrados nos aparecen descompuestos en triángulos iguales. Rellena:

El área del cuadrado del cateto 1 tiene ___ triángulos iguales

El área del cuadrado del cateto 2 tiene ___ triángulos iguales

El área del cuadrado de la hipotenusa tiene ___ triángulos iguales

Repite la operación con otro triángulo rectángulo de distinta dimensión que encuentres en la representación. Te damos dos ejemplos más:

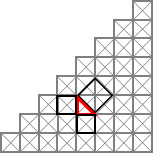
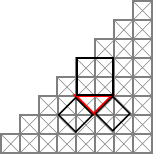
¿Ves alguna relación entre las áreas de los cuadrados que se obtienen en este proceso? ¿Te atreves a enunciar una “regla general”? Inténtalo

Ternas pitagóricas son conjuntos de tres números, por ejemplo 5, 4 y 3, que verifican la relación $a^2=b^2+c^2$. Hay muchas más. ¿Nos valdría cualquier terna de números? Trabajando en grupo, intentad encontrar más conjuntos de tres números que verifiquen esa relación.

Si esos números que forman ternas pitagóricas y verifican la expresión algebraica $a^2=b^2+c^2$ corresponden a las medidas de los lados de un triángulo, sabemos que el triángulo es rectángulo.  Tendremos enunciado para el Teorema de Pitágoras:

En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos:

$a^2=b^2+c^2$

El Teorema de Pitágoras tiene también sus implicaciones geométricas. Nos habla de la relación entre las áreas de los cuadrados que se pueden construir en esos lados:

¿Y quizás algo más allá?

Además, tenemos que ser capaces de aplicarlo a situaciones reales y contextualizadas, identificando ángulos rectos, triángulos rectángulos, sus catetos e hipotenusa, y así poder resolver las cuestiones que se nos planteen.