Consideremos un cuadrado de lado $l$.

Si trazamos una diagonal del cuadrado, los ángulos agudos que forman el triángulo rectángulo formado por la diagonal y dos lados del cuadrado miden $45^{\circ}$

Aplicamos el teorema de Pitágoras para poner la diagonal en función del lado del triángulo:

$\begin{eqnarray*}d^{2} & = & l^{2}+l^{2}\\d^{2} & = & 2l^{2}\\d & = & \sqrt{2l^{2}}\\d & = & l\sqrt{2}\end{eqnarray*}$

Hallamos las razones trigonométricas de $45^{\circ}$:

• $\sin 45^{\circ}=\dfrac{l}{d}=\dfrac{l}{l\sqrt{2}}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$

• $\cos45^{\circ}=\dfrac{l}{d}=\dfrac{l}{l\sqrt{2}}=\dfrac{1}{\sqrt{2}}=\dfrac{\sqrt{2}}{2}$

• $\tan45^{\circ}=\dfrac{l}{l}=1$

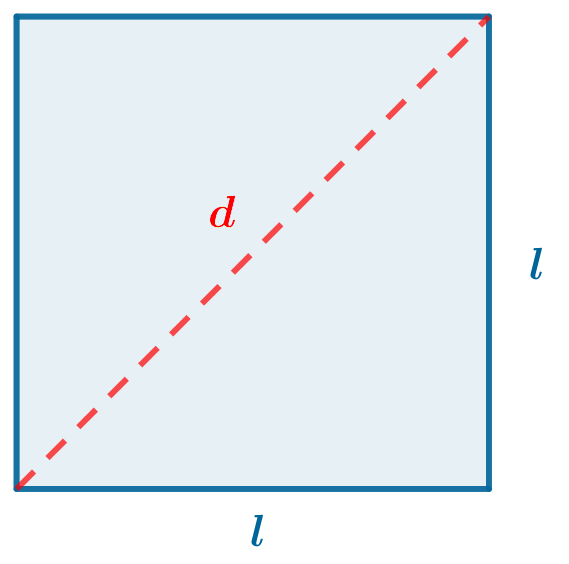
Para deducir las razones trigonométricas de un ángulo de $30^{\circ}$ nos apoyamos en un triángulo equilátero de lado $l$.

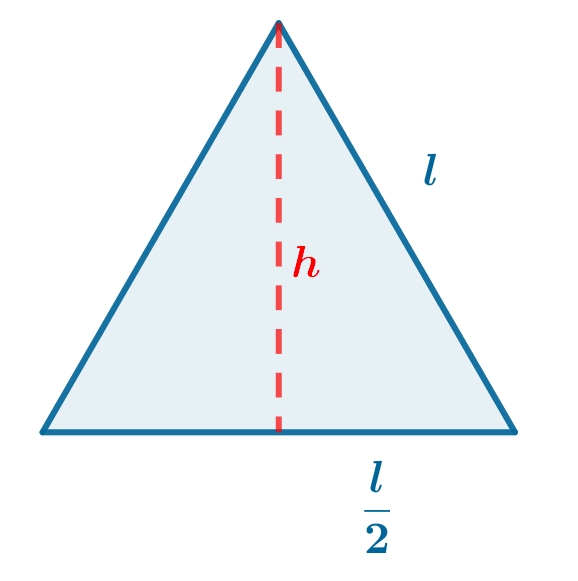
Primero, ponemos la altura del triángulo, $h$, en función del lado del triángulo, $l$, utilizando el teorema de Pitágoras:

$\begin{eqnarray*}
h^{2} & = & l^{2}-\left(\dfrac{l}{2}\right)^{2}\Leftrightarrow h^{2}=l^{2}-\dfrac{l^{2}}{4}\Leftrightarrow h^{2}=\dfrac{3l^{2}}{4}\Leftrightarrow h=\sqrt{\dfrac{3l^{2}}{4}}\Leftrightarrow h=\dfrac{l\sqrt{3}}{2}
\end{eqnarray*}$

Ahora, hallamos las razones trigonométricas de $30^{\circ}$:

• $\sin30=\dfrac{l/2}{l}=\dfrac{1}{2}$

• $\cos30=\dfrac{h}{l}=\dfrac{\frac{l\sqrt{3}}{2}}{l}=\dfrac{\sqrt{3}}{2}$

• $\tan30=\dfrac{l/2}{h}=\dfrac{\frac{l}{2}}{\frac{l\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}=\dfrac{\sqrt{3}}{3}$

Utilizamos el triángulo anterior para hallar las razones trigonométricas de $60^{\circ}$:

• $\sin60=\dfrac{h}{l}=\dfrac{\frac{l\sqrt{3}}{2}}{l}=\dfrac{\sqrt{3}}{2}$

• $\cos60=\dfrac{l/2}{l}=\dfrac{1}{2}$

• $\tan60=\dfrac{h}{\frac{l}{2}}=\dfrac{\frac{l\sqrt{3}}{2}}{\frac{l}{2}}=\sqrt{3}$